Stichprobengröße berechnen
Erleichtern Sie sich die Arbeit mit unserem präzisen Stichprobenrechner und erfahren Sie, wie Sie die Stichprobengröße berechnen. Sie möchten gerne noch mehr erfahren? Dann sehen Sie sich unsere Features und Umfragevorlagen an, die belastbare Ergebnisse liefern.

Stichprobengröße berechnen
Populationsgröße
Konfidenzniveau (%)
Fehlerspanne (%)
Stichprobengröße
383
Betreiben Sie Marktforschung? SurveyMonkey Audience liefert Ihnen schnell und bequem die richtigen Teilnehmenden für Umfragen. Anhand demografischer Angaben, Verbraucherverhalten, Geografie oder sogar eines bestimmten Marketingbereichs können Sie leicht die passende Zielgruppe festlegen.
Wie viele Teilnehmende benötigen Sie für Ihre Umfrage? Mit unserem Stichprobenrechner erfassen Sie ganz einfach die nötige Anzahl an Beantwortungen.
Was bedeutet Stichprobengröße bzw. Stichprobenumfang?
Die Anzahl der abgeschlossenen Beantwortungen, die Ihre Umfrage erhält, ist die Stichprobengröße. Sie sollte die Zielpopulation repräsentieren, deren Meinung und Verhalten für Sie wichtig ist.
Sehen wir uns folgende Punkte genauer an:
- die verschiedenen Möglichkeiten, die Ergebnisse für Ihre Stichprobe zu interpretieren
- die Formel zur Berechnung der Stichprobengröße
- weshalb eine angemessene Stichprobengröße für eine Umfrage wichtig ist
- wie sich die Bedeutung der Stichprobengröße je nach Umfragetyp unterscheidet
- bewährte Methoden für die Berechnung der Stichprobengröße
Welche Daten benötigen Sie, um die Stichprobengröße berechnen zu können?
Die folgenden Schlüsselbegriffe sollten Sie verstehen, damit Sie die Stichprobengröße berechnen können:
Die Populationsgröße ist die Gesamtzahl der Personen in der Gruppe, die Sie untersuchen möchten. Wenn Sie Menschen in Deutschland befragen möchten, läge die Populationsgröße bei etwa 83,6 Millionen. Bei Umfragen in Ihrem Unternehmen entspräche die Populationsgröße der Gesamtzahl der Beschäftigten.
Die Fehlerspanne ist ein Prozentsatz, der angibt, wie genau Umfrageergebnisse die Meinungen der Gesamtpopulation widerspiegeln. Je niedriger die Fehlerspanne, desto genauer ist die Antwort auf einem bestimmten Konfidenzniveau.
Mehr zum Thema: Fehlerspanne berechnen (mit Formel und Beispielen)
Das Konfidenzniveau gibt an, wie sicher Sie sein können, dass die Population eine Antwort innerhalb eines bestimmten Bereichs auswählen wird. Beispielsweise bedeutet ein Konfidenzniveau von 95 % für Sie eine Sicherheit von 95 %, dass die Resultate zwischen den Zahlen X und Y liegen.
Das Konfidenzintervall stellt einen statistischen Wertebereich dar, der das tatsächliche Ergebnis mit einer bestimmten Wahrscheinlichkeit enthält. Ein Konfidenzintervall von 95 % besagt beispielsweise, dass wenn Sie aus derselben Population mehrmals eine Stichprobe ziehen, das tatsächliche Ergebnis bei ca. 95 % der Stichproben innerhalb des Intervalls liegen würde.
So berechnen Sie die Stichprobengröße
Wie ermitteln Sie die minimale Stichprobengröße für Ihre Befragung? Wenn Sie diesen Wert selbst berechnen möchten, verwenden Sie folgende Formel:
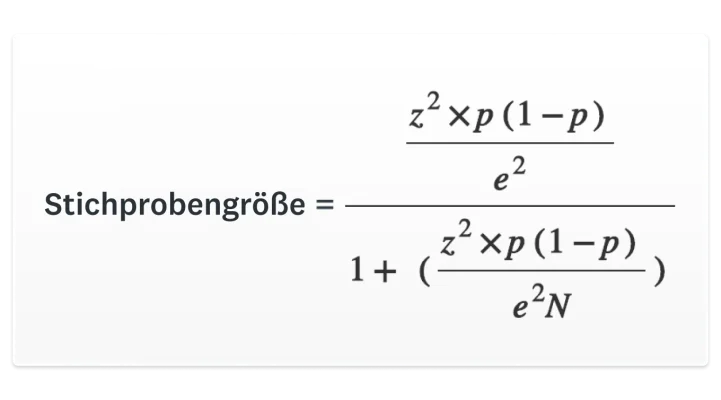
N = Populationsgröße • e = Fehlerspanne (Prozent im Dezimalformat) • z = Z-Wert
Der Z-Wert entspricht der Standardabweichung, die ein bestimmter Anteil vom Mittelwert entfernt ist. Den jeweils richtigen Z-Wert können Sie der nachstehenden Tabelle entnehmen:
| Gewünschtes Konfidenzniveau | Z-Wert |
| 80 % | 1,28 |
| 85 % | 1,44 |
| 90 % | 1,65 |
| 95 % | 1,96 |
| 99 % | 2,58 |
Stichprobengröße berechnen: reale Beispiele
Sehen wir uns einige Beispiele zur Berechnung der Stichprobengröße an:
Beispiel 1: Feedback zu Lieferdiensten
Angenommen, Sie möchten in einer Stadt mit 500.000 Einwohnern Feedback zu Lieferdiensten erhalten. Der Stichprobenumfang soll ein Konfidenzniveau von 95 % und eine Fehlerspanne von 5 % haben. Unter Verwendung der Formel (oder des Rechners oben) ermitteln Sie eine Stichprobengröße von 384.
Beispiel 2: unternehmensweite Befragung
Wenn Sie hingegen eine firmenweite Befragung mit 300 Angestellten durchführen und ein Konfidenzniveau von 80 % und eine Fehlerspanne von 10 % wünschen, beträgt die Stichprobengröße 37.
Hierauf müssen Sie beim Berechnen des Stichprobenumfangs achten:
- Wenn Sie eine kleinere Fehlerspanne möchten, bedeutet dies, dass Sie bei gleicher Population eine größere Stichprobengröße benötigen.
- Je höher das gewünschte Konfidenzniveau der Stichprobe, desto größer muss die Stichprobengröße sein.
Was ist eine gute Stichprobengröße?
Die Stichprobengröße Ihrer Erhebung hängt häufig vom Ziel und von der Population ab, die Sie befragen möchten.
So kann es beispielsweise ausreichend sein, nur ausgewählte Kundinnen und Kunden zu befragen, wenn es um eine Umfrage zum Kundenfeedback geht. Bei der politischen Meinungsforschung dagegen muss eine Stichprobe ausgewählt werden, die sowohl eine angemessene Größe hat als auch repräsentativ ist, um die Gesamtbevölkerung akkurat widerzuspiegeln.
So können sich die einzelnen Werte auf Ihre Befragung auswirken:
Wirkung der Umfragewerte auf die Genauigkeit der Ergebnisse
| Höherer Wert | Niedrigerer Wert | |
| Populationsgröße | Genauigkeit nimmt ab | Genauigkeit nimmt zu |
| Stichprobengröße | Genauigkeit nimmt zu | Genauigkeit nimmt ab |
| Konfidenzniveau | Genauigkeit nimmt zu | Genauigkeit nimmt ab |
| Fehlerspanne | Genauigkeit nimmt ab | Genauigkeit nimmt zu |
Stichprobengröße berechnen nach Umfragetyp
Je nach Anwendungsfall kann entschieden werden, ob eine statistisch signifikante Stichprobengröße verwendet werden sollte:
- Befragungen zur Mitarbeiterzufriedenheit bieten wichtige Einblicke in deren Stimmung. Eine statistisch signifikante Stichprobengröße kann einen umfassenderen Überblick ermöglichen, aber für die Ermittlung des Optimierungspotenzials im Arbeitsumfeld sind kleinere Stichproben sehr hilfreich.
- Für Kundenzufriedenheitsumfragen ist nicht immer eine große Stichprobe erforderlich. Die Genauigkeit und die Repräsentativität der Kundenstimmung sind hingegen wichtig, und die genaue Prüfung der Beantwortungen ist besonders entscheidend für das Geschäft. Jedes Feedback, ob positiv oder negativ, ist von Bedeutung.
- Marktforschungsumfragen benötigen eine ausreichend große Stichprobe, um wichtige Erkenntnisse über Ihre Kundschaft und Ihren Zielmarkt zu erhalten. Dadurch wird sichergestellt, dass Sie effektiv fundierte Informationen erfassen, die Ihren Zielmarkt repräsentieren.
- Bildungsumfragen sollten über eine statistisch signifikante Stichprobengröße verfügen, um aussagekräftige Erkenntnisse zu gewährleisten. Allerdings ist eine statistisch signifikante Stichprobe möglicherweise weniger wichtig, wenn das Ziel lediglich darin besteht, Feedback von Lernenden zu erfassen.
- Gesundheitsumfragen benötigen eine statistisch signifikante Stichprobengröße, um die Belange der Patientinnen und Patienten zu erkennen und die medizinische Forschung voranzubringen. Für die Erhebung der Patientenzufriedenheit oder die Beurteilung der Routineversorgung kann die Stichprobe auch kleiner sein.
- Lustige Umfragen sind witzige Fragen oder lustige Tests, die Sie an Freund:innen, Kolleg:innen oder Familienmitglieder versenden können. Für diese Spaßumfragen ist eine statistisch signifikante Stichprobengröße in aller Regel nicht erforderlich.
Was ist eine große Stichprobe?
Es gibt keinen allgemein gültigen Standard für die Bestimmung einer großen Stichprobe. Die Stichprobengröße variiert häufig je nach Kontext, z. B. Fachgebiet oder Forschungsziel.
Eine große Stichprobe bietet in der Regel genügend statistische Aussagekraft, um aussagekräftige Unterschiede in der untersuchten Population zu erkennen. In vielen Bereichen werden Stichproben mit Hunderten von Personen von Fachleuten als groß erachtet.
Allerdings entscheiden die Marktforschenden basierend auf Faktoren wie statistischer Aussagekraft oder verfügbare Ressourcen, wie viele Teilnehmende sie auswählen möchten. Die Größe Ihrer Stichprobe kann auch von der Art der Analyse abhängen, die Sie durchführen. Für einige statistische Tests sind möglicherweise größere Stichproben erforderlich als für andere.
Außerdem sollten Sie bedenken, dass die Größe der Stichprobe auch von der Komplexität der Population abhängen kann. Bei sehr vielfältigen Populationen oder bei der Untersuchung seltener Phänomene kann eine größere Stichprobe erforderlich sein.

Stichprobengröße berechnen: Best Practices
Mithilfe dieser Tipps können Sie die optimale Stichprobengröße für Ihre Befragung berechnen:
Legen Sie das Ziel Ihrer Befragung fest
Der Zweck der Datenerhebung ist für die Stichprobengröße wichtig. Wenn die Stichprobe zu klein ist, sind die Ergebnisse der Umfrage möglicherweise nicht genau. Wenn sie zu groß ist, kann die Erhebung teuer werden oder mehr Zeit in Anspruch nehmen.
Beim Erfassen von Umfragedaten benötigen Sie möglicherweise eine größere Stichprobe, um fundierte Resultate zu erhalten oder die Ergebnisse auf eine größere Gruppe anzuwenden. Kleinere Stichproben könnten ausreichen, wenn Sie die Befragungsdaten hauptsächlich für qualitative Erkenntnisse nutzen möchten.
Arbeiten Sie innerhalb von Budgets und Zeitvorgaben
Größere Stichproben können aufgrund des Aufwands zur Datenerfassung, Teilnehmeranreize und Analyse teurer sein. Bei einem kleineren Budget könnte eine kleinere Stichprobe angemessen sein. Auch zeitliche Beschränkungen können die Stichprobengröße beeinflussen.
Haben Sie nicht viel Zeit für die Befragung, dann ist eine kleinere Stichprobengröße besser, um die Daten schnell zu erfassen. Haben Sie hingegen mehr Zeit haben, sollten Sie eine größere Stichprobe auswählen, um die Genauigkeit Ihrer Resultate zu erhöhen.
Berücksichtigen Sie den Umfragetyp
Unterschiedliche Umfragetypen können unterschiedliche Herangehensweisen an die Stichprobengröße erforderlich machen. Umfragen zum Kundenfeedback funktionieren mit kleineren Stichproben. Für politische Umfragen hingegen sind größere und repräsentativere Stichproben erforderlich. Passen Sie Ihre Herangehensweise an, um sicherzustellen, dass die Ergebnisse statistisch fundiert und zuverlässig sind.
Setzen Sie offene Fragen mit Bedacht ein
Bei offenen Fragen müssen detaillierte Antworten eingegeben werden. Dadurch dauert die Beantwortung der Erhebung länger, weil die Befragten mehr schreiben müssen. Dies kann dazu führen, dass einige Teilnehmende die Umfrage nicht abschließen, wodurch es schwieriger wird, eine große Stichprobe zu erreichen. Passen Sie die Anzahl der offenen Fragen an oder planen Sie die Stichprobengröße entsprechend.
Häufige Fehler bei der Stichprobengröße
Vermeiden Sie häufige Fehler, wenn Sie die Stichprobengröße berechnen. Denn dadurch kann die Effektivität Ihrer Befragung beeinträchtigt werden. Dies könnten insbesondere folgende Punkte sein:
- Fehlerspanne nicht berücksichtigt: Die Fehlerspanne gibt den Grad der Präzision und Zuverlässigkeit der Umfrageergebnisse an. Wird die Fehlerspanne nicht berücksichtigt, ist die Stichprobe am Ende vielleicht nicht ausreichend groß und die Schlussfolgerungen sind weniger zuverlässig.
- Unzureichendes Konfidenzniveau: Das Konfidenzniveau gibt den Grad der Sicherheit des erwarteten Resultats an. Wenn kein angemessenes Konfidenzniveau festgelegt wird, kann dies die Genauigkeit der Umfrageergebnisse beeinträchtigen.
- Nicht kompatibler Umfragetyp: Für unterschiedliche Umfragetypen sind unterschiedliche Stichprobengrößen abhängig vom gewünschten Grad an Genauigkeit und Präzision erforderlich.
- Nutzung zu kleiner Stichproben: Die Verwendung einer zu kleinen Stichprobe ohne Berücksichtigung der statistischen Aussagekraft kann zu verzerrten und nicht repräsentativen Ergebnissen führen.
Häufig gestellte Fragen (FAQs)
- Was bedeutet Stichprobengröße bzw. Stichprobenumfang?
- Was benötige ich, um die Stichprobengröße für meine Befragungen zu berechnen?
- Wie berechne ich die Stichprobengröße für meine Umfrage?
- Was bedeutet eine große Stichprobe in Bezug auf Umfragen?
Erhalten Sie schneller mehr Antworten
Verwenden Sie unseren Stichprobenrechner, um fundiertere Umfrageergebnisse zu erzielen. Benötigen Sie mehr Befragte, dann verwenden Sie SurveyMonkey Audience. Dadurch erreichen Sie Umfrageteilnehmende weltweit und bekommen Antworten von nahezu jeder gewünschten Zielgruppe.
Weitere Ressourcen entdecken

Insights Manager
Insights Manager können mithilfe dieses Toolkits umsetzbare Erkenntnisse liefern, um Stakeholder zu unterstützen und die richtigen Zielgruppen zu erreichen.

3 Trends am Arbeitsplatz, die die Arbeitswelt von heute verändern
Studien zu Trends am Arbeitsplatz und dazu, wie Mitarbeitende ihre private Zeit einteilen, im Homeoffice arbeiten und zur Kombination Homeoffice und Büro

3 Mythen über die Marktforschung – widerlegt durch SurveyMonkey
Weitverbreitete Irrtümer und Mythen über die Marktforschung werden durch die Lösungen von SurveyMonkey erfolgreich widerlegt.

Geschlossene Fragen: Beispiele und Anwendungsfälle
Was ist eine geschlossene Frage und wie erhalten Sie quantitative Daten? Hier finden Sie alles, was Sie wissen sollten, einschließlich Frage- und Umfragebeispiele.
Benötigen Sie mehr Beantwortungen für Ihre Umfrage?
Nutzen Sie SurveyMonkey Audience, unser globales Umfragepanel von Millionen Menschen, die Ihnen gerne ihre Meinung mitteilen.