Repräsentative Stichprobe berechnen: Formeln, Beispiele und Tipps
Durch die Auswahl der richtigen Teilnehmer können Sie die Zuverlässigkeit von Umfrageergebnissen steigern.
Umfragen und Stichproben gelten immer dann als besonders aussagekräftig, wenn sie repräsentativ sind. Doch oftmals ist nicht genau klar, was eine repräsentative Stichprobe auszeichnet und wie sie zu erhalten ist.
Was ist eine repräsentative Stichprobe? Eine Definition
Repräsentativ ist eine Stichprobe dann, wenn sie so gewählt ist, dass allgemeingültige Rückschlüsse gezogen werden können. Das bedeutet: Die Stichprobe ist so zusammengesetzt, dass sie die Gesamtzielgruppe in allen wichtigen Merkmalen widerspiegelt. Damit das der Fall ist, müssen drei grundlegende Voraussetzungen erfüllt werden.
Voraussetzungen für eine repräsentative Stichprobe
- Passende Definition der Grundgesamtheit (Wer wird befragt? Welche Merkmale zeichnen die Zielgruppe aus?)
- Verwendung eines Zufallsverfahrens zur Auswahl
- Festlegung einer adäquaten Auswahlgrundlage (Art der Untersuchung/Befragung)
Welche Probleme kann es bei der Auswahl einer repräsentativen Stichprobe geben?
In der Praxis ist es nicht immer ganz einfach, die Bedingungen für eine repräsentative Stichprobe zu erfüllen. Wer beispielsweise eine Telefonumfrage startet, um die generelle Stimmungslage zu einem lokalpolitischen Thema zu ermitteln, kann zwar zufällig ausgewählte Nummern aus dem Telefonbuch anrufen. Viele Menschen besitzen jedoch inzwischen keinen Festnetzanschluss mehr, heben bei einer unbekannten Nummer den Hörer nicht ab oder sind nicht im Telefonbuch eingetragen. Sie würden in diesem Fall mit großer Wahrscheinlichkeit keine repräsentative Stichprobe erhalten, sondern lediglich einzelne Meinungen, die keinen Rückschluss auf das große Ganze zulassen – selbst wenn alle Angerufenen der gleichen Meinung wären. Eine so entstehende Über- oder Unterschätzung des Ergebnisses wird als „Bias“ bezeichnet und ist die Differenz zwischen den abgeleiteten und den tatsächlichen Werten der Grundgesamtheit.
Bias kann zum Beispiel entstehen durch:
- Verweigerung der Teilnahme durch bestimmte Teile der Grundgesamtheit
(z. B. aus Scham, Angst etc.) - Fehler im Zufallsverfahren/Heterogenität der Auswahlwahrscheinlichkeiten (z. B. Berufstätige, die tagsüber nicht zu Hause erreichbar sind, etc.)
- Nichterreichbarkeit bestimmter Gruppen der Grundgesamtheit (z. B. kein Festnetzanschluss, kein Internetzugang, kein Social-Media-Profil etc.)
- Generelle Fehler in der Erhebungsmethode und Auswahl
Wann ist eine repräsentative Stichprobe sinnvoll oder notwendig?
Eine Umfrage und die dafür gewählte Stichprobe muss immer dann repräsentativ sein, wenn aus der Analyse der Stichprobe verallgemeinerbare Aussagen abgeleitet werden sollen. Das ist zum Beispiel bei den klassischen Sonntagsumfragen der Fall, in denen eine zufällig ausgewählte Gruppe an Wahlberechtigten danach gefragt wird, wem sie bei anstehenden Wahlen ihre Stimme geben würden. Auch im Bereich der Marktforschung kann eine repräsentative Umfrage innerhalb der gewünschten Zielgruppe sinnvoll sein, um die Beliebtheit einer Marke oder die Akzeptanz bestimmter Aktionen zu überprüfen. Sind Sie jedoch eher an individuellen Meinungen und Erfahrungen interessiert, muss die Stichprobe nicht zwangsläufig repräsentativ sein.
| Wann sind repräsentative Stichproben sinnvoll? | Wann sind repräsentative Stichproben nicht nötig? |
| Sehr große Grundgesamtheit | Überschaubare Grundgesamtheit, bei der jeder Einzelne befragt werden kann |
| Wunsch nach Allgemeingültigkeit der Ergebnisse | Fokus auf individuelle Erfahrungen (bspw. Kundenfeedbacks) |
Wie lässt sich eine repräsentative Stichprobe berechnen?
Wie viele Menschen müssen denn nun befragt werden, damit die Stichprobe und das Ergebnis als repräsentativ gelten? Eine pauschale Antwort gibt es darauf nicht. Natürlich gilt das Motto „Je mehr, desto besser“, doch gerade bei groß angelegten, aufwendigen Umfragen kann der Umfang der Stichprobe ein nicht zu unterschätzender Kostenfaktor sein. Daher sollte das Ziel nicht sein, so viele Menschen wie möglich zu befragen, sondern so viele wie nötig. Bei Umfragen, die die Bundesrepublik Deutschland betreffen, werden meistens 1.000 Leute herangezogen, die als Stellvertreter für die rund 80 Millionen Einwohner fungieren. Für alle anderen Umfragen gibt es zwei Möglichkeiten, um die richtige Stichprobengröße zu berechnen: die Nutzung einer passenden Formel oder der Einsatz eines Online-Rechners.
Dabei ist jedoch eines zu bedenken: Das Problem des Bias lässt sich auch mit einem größeren Stichprobenumfang nicht beseitigen. Dafür muss an den entsprechenden Stellschrauben in der Methodik gedreht werden.
Möglichkeit 1: Repräsentative Stichprobe berechnen mit der passenden Formel
Um die notwendige Größe der Stichprobe zu berechnen, müssen einige Werte und Zahlen vorliegen.
- Die Populationsgröße oder Grundgesamtheit (N) umfasst alle Menschen, die für die Stichprobe infrage kommen.
- Die Fehlerspanne oder das Konfidenzintervall (e) gibt an, wie hoch die Wahrscheinlichkeit ist, dass die Antworten der Stichproben denen der Grundgesamtheit entsprechen.
- Das Konfidenzniveau zeigt, mit welcher Wahrscheinlichkeit die Stichprobe die Population repräsentiert. Je höher das Konfidenzniveau, desto höher die Genauigkeit.
- Aus dem Konfidenzniveau lässt sich der Z-Wert ableiten. Die Berechnung des Z-Werts ist kompliziert, sodass hier auf bestehende Tabellen zurückgegriffen werden sollte.
- Der letzte benötigte Wert ist die Standardabweichung (p). Sie gibt an, wie groß die Varianz der Ergebnisse voraussichtlich sein wird. Da dieser Faktor vor der Umfrage normalerweise nicht bekannt ist, wird mit einer Standardabweichung von 50 % gearbeitet. Diese stellt den „Worst Case“ da.
Sind all diese Werte vorhanden, können sie in einer Standardformel für kleinere und mittlere Populationen verwendet werden:
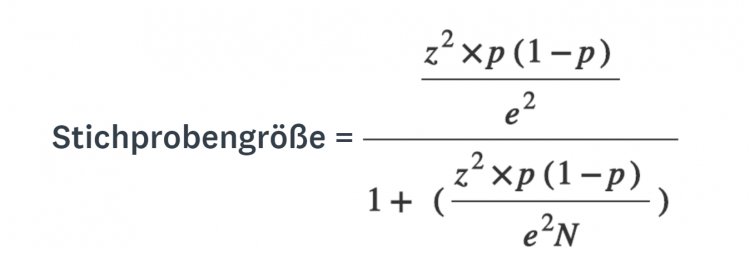
Bei größeren Populationen oder wenn die Größe der Grundgesamtheit unbekannt ist, kann auch nur der obere Teil der Formel zur Berechnung genutzt werden.
Möglichkeit 2: Repräsentative Stichprobe berechnen mit Online-Tools
Wenn die Auseinandersetzung mit Z-Werten und Konfidenzintervallen sowie die Berechnung der Stichprobengröße per Hand zu komplex erscheinen, kann der Stichprobenrechner von SurveyMonkey weiterhelfen. Hier müssen Sie lediglich die Populationsgröße, das gewünschte Konfidenzniveau und die akzeptierte Fehlerspanne eingeben, um eine Größe für die repräsentative Stichprobe zu erhalten.
Berechnung einer repräsentativen Stichprobe: Beispiel Studentenbefragung
Sie möchten im Rahmen einer repräsentativen Umfrage herausfinden, wie gut das Mensaangebot der Universität bei den Studierenden ankommt. Dafür legen Sie folgende Werte fest:
N = 5.000 (Summe aller eingeschriebenen Studierenden)
e = 0,1 (erlaubte Fehlermarge von +/-10 %)
Konfidenzniveau: 95 %, resultierender Z-Wert: 1,96
p = 0,5 (Standardabweichung von 50 %)
Daraus ergibt sich:

Demnach wäre eine Stichprobengröße von 95 zufällig ausgewählten Studierenden notwendig, damit die Umfrage unter den gegebenen Umständen als repräsentativ gelten kann. Eine solche Umfrage zur Kundenzufriedenheit – denn die Studierenden sind in diesem Fall nichts anderes als Kunden – können Sie zum Beispiel mithilfe unserer Umfragevorlagen zur Kundenzufriedenheit schnell und einfach erstellen.