t-Tests im Detail: ihre Bedeutung für die Umfrageanalyse

Der Unterschied zwischen zwei Zahlen ist zwar für jeden ersichtlich, doch zu ermitteln, ob diese Differenz tatsächlich statistisch signifikant ist, kann schon etwas mehr Arbeit bedeuten.

Angenommen, Sie haben eine Umfrage zur Kundenzufriedenheit für Ihr Unternehmen durchgeführt und haben eine Menge Ergebnisse zu analysieren. Sie fragen Ihre Vorgesetzte, was Sie zuerst analysieren sollen, und sie möchte wissen, ob Männer und Frauen unterschiedliche Antworten geben. Etwa, ob Männer Ihrem Unternehmen im Schnitt einen niedrigeren Net Promoter Score℠ (NPS) geben als Frauen.

Wenn Sie die Daten untersuchen, erkennen Sie, dass die durchschnittliche Bewertung von männlichen Befragten bei 9 liegt, während die durchschnittliche Bewertung von weiblichen Befragten bei 12 liegt. Woher sollen Sie nun wissen, ob sich 9 signifikant von 12 unterscheidet? Genau hier kommt der t-Test ins Spiel.

Der t-Test ist eine Möglichkeit, zu ermitteln, ob sich zwei Zahlen signifikant voneinander unterscheiden. Es gibt verschiedene Arten von t-Tests, und jeder wird mit einer anderen Formel berechnet.

1. Einstichproben-t-Test: Bei diesem Test wird ermittelt, ob der Mittelwert (bzw. Durchschnitt) von Daten aus einer Gruppe (in diesem Fall der Gesamt-NPS) sich von einem von Ihnen angegebenen Wert unterscheidet.

Beispiel: Ziel Ihres Unternehmens ist es, einen NPS zu haben, der signifikant höher ist als der Branchenstandard von 5. Die letzte Umfrage Ihres Unternehmens ergab einen NPS von 10. Ist ein NPS von 10 signifikant höher als der Branchenstandard von 5?

2. Zweistichproben-t-Test: Bei diesem Test wird untersucht, ob sich die Mittelwerte von zwei unabhängigen Gruppen signifikant voneinander unterscheiden.

Beispiel: Ihre Hypothese ist es, dass Männer Ihrem Unternehmen einen niedrigeren NPS geben als Frauen. Der durchschnittliche NPS von männlichen Befragten liegt bei 9, während die durchschnittliche Bewertung von Frauen bei 12 liegt. Unterscheidet sich 9 signifikant von 12?

3. Gepaarter t-Test: Diesen Test führen Sie durch, wenn Sie derselben Personengruppe dieselbe Umfrage zweimal vorlegen. Durch einen gepaarten t-Test erfahren Sie, ob sich der Mittelwert zwischen der ersten und der zweiten Umfrage verändert hat.

Ein Beispiel: Sie haben dieselbe Gruppe von Kunden zweimal befragt: einmal im April und ein zweites Mal im Mai, nachdem diese Kunden eine Anzeige Ihres Unternehmens gesehen hatten. Hat sich der NPS Ihres Unternehmens verändert, nachdem die Kunden die Anzeige gesehen hatten?

Hier ist zu beachten, dass Sie anhand von t-Tests zwar ermitteln können, ob ein signifikanter Unterschied vorliegt, doch liegt es immer noch an Ihnen, zu bestimmen, ob dieser Unterschied bedeutsam ist. Kleine Unterschiede können statistisch signifikant sein, wenn die Stichprobengröße groß genug ist.

Die Durchführung eines t-Tests umfasst 4 Schritte:

1. Berechnen des t-Werts:
Jede Art von t-Test hat eine andere Formel zur Berechnung des t-Werts (unten auf der Seite finden Sie alle drei Formeln).

2. Berechnen der Freiheitsgrade: 
Freiheitsgrade geben über die Anzahl der Möglichkeiten Auskunft, wie der Mittelwert variieren kann. In diesem Fall sind die Freiheitsgrade die Anzahl der NPS-Bewertungen, die in einer vorgegebenen Gruppe von Befragten vorkommen kann. Ähnlich wie der t-Wert unterscheidet sich die Formel für die Freiheitsgrade abhängig von der Art des t-Tests, den Sie durchführen.

3. Ermitteln des kritischen Werts: 
Der kritische Wert ist die Schwelle, an der die Differenz zwischen zwei Zahlen als statistisch signifikant betrachtet wird und damit auch der T-test signifikant ist.

4. Vergleichen des Absolutwerts des t-Werts mit dem kritischen Wert: 
Wenn Ihr t-Wert größer ist als der kritische Wert, ist die Differenz signifikant. Wenn Ihr t-Wert kleiner ist, dann sind Ihre zwei Zahlen statistisch gesehen ununterscheidbar.

Gehen wir einmal von Anfang an durch das Beispiel: Ihre Hypothese ist es, dass Männer Ihrem Unternehmen einen niedrigeren NPS geben als Frauen. Der durchschnittliche NPS von Männern liegt bei 9, während die durchschnittliche Bewertung von Frauen bei 12 liegt. Unterscheidet sich 9 signifikant von 12? Dies ist ein gutes Beispiel für den Einsatz eines Zweistichproben-t-Tests.

1. Berechnen des t-Werts: 

Nachstehend ist die Formel für den Zweistichproben-t-Test mit folgenden Eigenschaften aufgeführt:

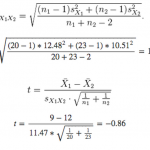
2. Berechnen der Freiheitsgrade: 

Diese Formel muss angewendet werden, um Freiheitsgrade in Zweistichproben-t-Tests zu bestimmen. Die Formeln für sonstige Arten von Tests werden nachfolgend aufgeführt.

3. Ermitteln des kritischen Werts: 

Nach dieser Tabelle liegt bei einem zweiseitigen t-Test mit einem Alpha-Niveau von 0,05 bei 41 Freiheitsgraden der kritische Wert bei 2,02. Beachten Sie, dass die meisten Analysten statt eines einseitigen t-Tests einen zweiseitigen t-Test verwenden, da dieser konservativer ist. Weitere Informationen zu den Unterschieden zwischen einseitigen und zweiseitigen t-Tests finden Sie in diesem Video der Khan Academy.

4. Vergleichen des Absolutwerts des t-Werts mit dem kritischen Wert: 

Da der Absolutwert des t-Werts 0,86 beträgt und damit nicht größer ist als der kritische Wert von 2,02, können Sie schließen, dass Männer keine signifikant niedrigere NPS-Bewertung als Frauen vergeben.

Sie führen Ihre t-Tests wahrscheinlich in einem Tabellenkalkulationsprogramm oder in einem Statistikprogramm (wie Excel oder SPSS) durch. Doch wenn Sie von Hand rechnen möchten, finden Sie nachfolgend die Formeln für die beiden sonstigen Arten von t-Tests.

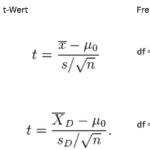
Wenn Sie sich dafür entscheiden (wie die meisten es tun), Ihre t-Tests in einem Tabellenkalkulationsprogramm oder in einem Statistikprogramm durchzuführen, unterscheidet sich der Vorgang geringfügig. Statt den t-Wert mit dem kritischen Wert zu vergleichen, berechnen die meisten Programme einen p-Wert, der dann mit dem Alpha-Niveau verglichen wird (das am häufigsten verwendete Niveau ist 0,05). In diesem Fall weist dann ein p-Wert kleiner als das Alpha-Niveau darauf hin, dass sich die Zahlen signifikant unterscheiden.

Net Promoter Score ist eine Marke von Bain & Company, Inc., Satmetrix Systems, Inc. und F. Reichheld.