Fehlerspanne berechnen: Formeln und Beispiele
Erfahren Sie, wie Sie die Fehlerspanne berechnen und nutzen Sie zur Ermittlung unseren präzisen Fehlermargenrechner.
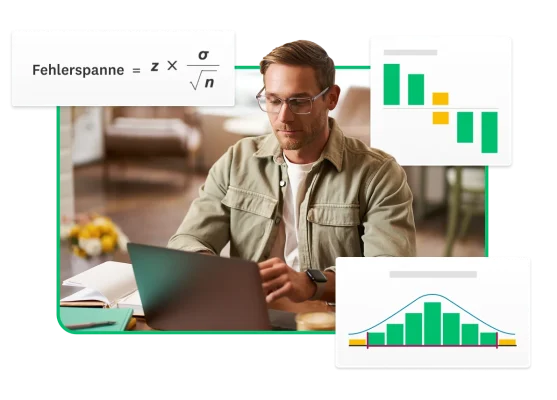
- Die Fehlerspanne oder auch Fehlermarge bzw. Irrtumswahrscheinlichkeit zeigt Ihnen, in welchem Maße Sie erwarten können, dass Ihre Umfrageergebnisse für die Ansichten der betrachteten Gesamtpopulation repräsentativ sind.
- Die Fehlerspanne wird mithilfe dieser Elemente berechnet: n = Stichprobengröße, σ = Standardabweichung der Grundgesamtheit, z = z-Wert (Sie können auch den unten stehenden Rechner verwenden).
- Mit dem Fehlerspannenrechner ermitteln Sie, ob Ihre Stichprobe groß genug ist, um mit einer gewissen Sicherheit sagen zu können, dass die erfassten Daten korrekt sind.
Fehlerspanne berechnen
Populationsgröße
Konfidenzniveau (%)
Stichprobengröße
Fehlerspanne
0
Was ist eine Fehlerspanne?
Erhebungen sind stets ein Balanceakt, denn Sie nutzen eine kleine Gruppe (die Befragten), um eine wesentlich größere Gruppe (Ihren Zielmarkt oder die Gesamtpopulation) zu repräsentieren. Die Fehlerspanne ist ein statistisches Mittel, das angibt, wie genau Umfrageergebnisse die Meinungen der Gesamtpopulation widerspiegeln.
Die Fehlermarge oder Irrtumswahrscheinlichkeit ist also ein Maß für die Genauigkeit Ihrer Umfrage. Je kleiner die Fehlerspanne, desto mehr Vertrauen können Sie in Ihre Ergebnisse haben; je größer, desto stärker sind die potenziellen Abweichungen von den Ansichten der Gesamtpopulation.
Wie der Name nahelegt, bezeichnet die Fehlerspanne einen Bereich von Werten über und unter den tatsächlichen Ergebnissen einer Befragung. Ein Beispiel: 60 % aller Befragten beantworten eine Frage mit „Ja“ und die Fehlermarge ist bei einem Konfidenzniveau von 95 % mit 5 % angegeben. Dann bedeutet dies, dass zwischen 55 % und 65 % der Gesamtpopulation diese Frage bejahen.
In der Forschung und der Demoskopie stellt die Fehlerspanne eine wesentliche Größe dar, da sie uns mitteilt, wie verlässlich unsere Ergebnisse sind. Mit ihrer Hilfe können wir bestimmen, zu welchem Grad unsere Erkenntnisse unsicher sind und sie ist damit eine wesentliche Metrik für die Interpretation der gewonnenen Daten. Je kleiner die Fehlerspanne, desto genauer sind die Daten und umso verlässlicher die Resultate. Größere Fehlermargen weisen auf mehr Variabilität und weniger Sicherheit der Ergebnisse hin.
Durch die Kenntnis der Fehlerspanne können Forschende und Führungskräfte fundiert die Verlässlichkeit ihrer Daten beurteilen.
Was ist ein Konfidenzintervall?
Konfidenzintervalle ermöglichen einzuschätzen, in welchem Bereich die tatsächlichen Resultate liegen. Angenommen, wir schätzen die Durchschnittsgröße von Erwachsenen in einem bestimmten Land. Dann liefert uns das Konfidenzintervall den Größenbereich, in dem der tatsächliche Durchschnitt mit hoher Sicherheit liegt.
Anhand von Konfidenzintervallen können Forschende und Führungskräfte ableiten, mit welcher Unsicherheit ihre Schätzungen und Analysen behaftet sind.
Welcher Zusammenhang besteht zwischen Fehlerspanne und Konfidenzintervallen?
Konfidenzintervalle und Fehlerspanne sind letztlich zwei verschiedene Wege, das Gleiche auszudrücken: mit welcher Unsicherheit eine Schätzung aus einer Erhebung verbunden ist. Während das Konfidenzintervall einen Wertebereich angibt, von dem wir sicher ausgehen können, dass die tatsächlichen Werte in diesem Bereich liegen, ist die Fehlerspanne ein Maß dafür, wie stark die Schätzung von dem tatsächlichen Wert abweichen könnte.
Das Konfidenzniveau folgt einem ähnlichen Konzept. Konfidenzniveaus geben einen Hinweis darauf, wie sicher Sie sein können, dass der tatsächliche Wert in dem Intervall liegt.
Gängige Konfidenzniveaus sind 90 %, 95 % und 99 %.Ein niedrigeres Konfidenzniveau liefert ein kleineres Konfidenzintervall. Je kleiner das Intervall, desto präziser ist unsere Schätzung. Aber bei einem niedrigem Konfidenzniveau ist es weniger wahrscheinlich, dass wir den tatsächlichen Wert erfassen. Im Gegenzug dazu liefert ein hohes Konfidenzniveau von beispielsweise 99 % ein größeres Konfidenzintervall. Dieses größere Intervall ist zwar weniger genau, aber der tatsächliche Wert wird mit einer höheren Wahrscheinlichkeit in genau diesem Bereich liegen.
Wann sollte die Fehlerspanne angewendet werden?
In Ihrer Umfrageplanung sollten Sie die Fehlermarge einsetzen, um möglichst genaue und verlässliche Resultate zu erzielen. Haben Sie das Konzept der Fehlerspanne verstanden, können Sie die Stichprobengröße berechnen, die Sie benötigen, damit Ihre Erhebungsschätzungen den gewünschten Genauigkeitsgrad haben. Bei kleineren Fehlermargen benötigen Sie eine größere Stichprobengröße. Umgekehrt reicht bei größeren Fehlerspannen schon eine kleinere Stichprobengröße .
Ein Beispiel: Sie möchten eine Befragung unter 100.000 Menschen durchführen. Ihre Fehlerspanne liegt bei ±5 % und Ihr Konfidenzniveau ist 95 %. Dann bräuchten Sie unter Verwendung der Standardberechnung eine Stichprobengröße von etwa 383 Befragten.
Darüber hinaus ist die Fehlermarge bei der Analyse der Ergebnisse wesentlich. Sie liefert ein Maß dafür, wie sicher (oder unsicher) die Resultate sind, und ermöglicht Forschenden wie Stakeholdern einzuschätzen, wie belastbar ihre Erkenntnisse sind.
Noch ein Beispiel: Eine Umfrage ergibt, dass 60 % der Befragten Produkt A dem Produkt B vorziehen, die Fehlerspanne liegt bei ±3 % und das Konfidenzniveau ist 95 %. So bedeutet dies, dass mit einer hohen Wahrscheinlichkeit (95 %) der tatsächliche Anteil der Menschen, die Produkt A bevorzugen, zwischen 57 % und 63 % liegt.
Mit welcher Formel lässt sich die Fehlerspanne berechnen?
Die Fehlermarge wird mit folgender Formel ermittelt:

n = Stichprobengröße • σ = Standardabweichung der Population • z = Z-Wert
- Nehmen Sie die Standardabweichung der Population (σ) und die Stichprobengröße (n). Der obige Fehlerspannenrechner geht von einer Standardabweichung aus, die auf der Quadratwurzel von p(1-p) basiert, wobei p der Stichprobenanteil und p=0,5 ein konservativer Standardwert ist.
- Nehmen Sie die Standardabweichung der Population und teilen Sie diese durch die Quadratwurzel Ihrer Stichprobengröße.
- Multiplizieren Sie das Ergebnis mit dem z-Wert, der mit Ihrem gewünschten Konfidenzniveau übereinstimmt (entsprechend der folgenden Tabelle):
| Gewünschtes Konfidenzniveau | Z-Wert |
| 80 % | 1,28 |
| 85 % | 1,44 |
| 90 % | 1,65 |
| 95 % | 1,96 |
| 99 % | 2,58 |
Fehlerspanne berechnen: Beispiel
Angenommen, Sie möchten eine Entscheidung zwischen einem Namen A und einem Namen B für ein neues Produkt treffen. Ihr Zielmarkt umfasst 400.000 potenzielle Kunden und Kundinnen. Dies ist Ihre Gesamtpopulation.
Nun beschließen Sie, 600 dieser potenziellen Kundinnen und Kunden zu befragen. Dies ist Ihre Stichprobengröße.
Da Resultat der Befragung zeigt, dass 60 % der Teilnehmenden den Namen A bevorzugen. Nun müssen Sie im Fehlerspannenrechner ein Konfidenzniveau angeben.
Dieser Wert drückt aus, mit welcher Sicherheit Sie sagen können, dass die Stichprobe die Einstellungen der Gesamtpopulation korrekt wiedergibt. Forscher:innen geben normalerweise einen Wert von 90 %, 95 % oder 99 % an.
Geben Sie doch einmal die Werte aus diesem Beispiel in den Fehlerspannenrechner oben ein. Sie erhalten dann eine Fehlermarge von 4 %.
Wissen Sie noch, dass sich 60 % Ihrer Befragten für den Namen A ausgesprochen hatten? Anhand der Fehlerspanne wissen Sie jetzt mit einer 95-prozentigen Konfidenz, dass 56 bis 64 % der Gesamtpopulation – also Ihres Zielmarkts – den Namen A für das Produkt bevorzugen würden.
Wir erhalten diese Werte – 56 und 64 –, indem wir die Fehlerspanne von den Antworten der Stichprobe subtrahieren bzw. dazu addieren.
Wie ist die Fehlerspanne zu interpretieren?
Die Fehlerspanne liefert einen Bereich von Werten über und unter den tatsächlichen Ergebnissen einer Erhebung. Ein Beispiel: Eine Umfrage zeigt, dass 60 % eine bestimmte Richtlinie unterstützen. Die Fehlerspanne liegt bei ±4 % und das Konfidenzniveau ist 95 %. Dann können wir mit einer vernünftigen Sicherheit davon ausgehen, dass der tatsächliche Grad der Unterstützung zwischen 56 % und 64 % liegt.
Größen, die die Fehlerspanne beeinflussen
1. Die Stichprobengröße
Die Stichprobengröße wirkt sich direkt auf die Fehlerspanne einer Befragung aus. Größere Stichproben haben in der Regel kleinere Fehlermargen und kleinere Stichproben größere Fehlerspannen.
So könnte beispielsweise eine Erhebung unter 1.000 Befragten eine Fehlerspanne von ±3 % haben. Eine Verdoppelung der Stichprobengröße auf 2.000 Teilnehmende könnte die Fehlermarge auf ±2 % reduzieren.
Passend dazu: Stichprobengröße berechnen
2. Das Konfidenzniveau
Höhere Konfidenzniveaus ziehen größere Fehlerspannen nach sich, während niedrigere Konfidenzniveaus kleinere Fehlermargen ermöglichen.
Ein Beispiel zur Verdeutlichung: Eine Umfrage mit einem Konfidenzniveau von 95 % könnte beispielsweise eine Fehlerspanne von ±3 % haben. Wird das Konfidenzniveau nun auf 99 % erhöht, könnte dies eine Fehlerspanne von ±4 % nach sich ziehen.
3. Die Variabilität der Population
Eine größere Variabilität der Population führt zu größeren und eine niedrigere Variabilität zu kleineren Fehlerspannen.
Nehmen wir dieses Beispiel zur Verdeutlichung: Die Schätzung des Haushaltsgesamteinkommens in einer Stadt, in der hohe Einkommensunterschiede herrschen, könnte eine größere Fehlerspanne erfordern, beispielsweise von ±5000 €. Für eine Stadt mit einer eher ausgeglichenen Einkommenssituation könnte eine kleinere Fehlermarge reichen, wie ±2000 €.
So erhalten Sie eine höhere Datenbelastbarkeit

Nun wissen Sie, wie die Fehlerspanne berechnet wird und wie sie sich auf Ihre Resultate auswirkt. Jetzt können wir uns ansehen, welche Schritte notwendig sind, damit Sie diese Konzepte in Ihrem Umfrageentwurf umsetzen können.
1. Bestimmen Sie Ihre Gesamtpopulation
Hierbei handelt es sich um die Anzahl der Personen, die Sie mit Ihrer Umfrage untersuchen möchten. Nehmen wir das obige Beispiel, so sind dies die 400.000 potenziellen Kund:innen.
2. Bestimmen Sie die Höhe des Risikos
Hier geben Sie an, wie groß das Risiko sein darf, dass sich Ihre Ergebnisse von den Einstellungen des gesamten Zielmarkts unterscheiden. Sie müssen also Fehlerspanne und Konfidenzniveau Ihrer Stichprobe berechnen.
3. Legen Sie die Stichprobengröße fest
Versuchen Sie, ein ausgewogenes Verhältnis zwischen Konfidenzniveau und akzeptabler Fehlerspanne zu finden, und entscheiden Sie auf dieser Grundlage, wie viele Befragte Sie benötigen. Sie müssen dabei einkalkulieren, dass längst nicht jede Person, der Sie die Erhebung schicken, sich auch daran beteiligen wird (Stichwort: Beantwortungsquote). Ihre Stichprobengröße ist die Anzahl der abgeschlossenen Beantwortungen, die Sie erhalten.
4. Berechnen Sie die Beantwortungsquote
Die Beantwortungsquote ist der prozentuale Anteil der Befragten, die eine Erhebung auch tatsächlich komplett abschließen. Ziehen Sie zur Ermittlung der üblichen Beantwortungsquote frühere Befragungen heran. Wenn Sie keine Daten aus vorherigen Erhebungen haben, stellen Sie eine fundierte Vermutung an. Eine konservative allgemeine Schätzung ist, dass etwa 10 % bis 15 % eine Umfrage abschließen.
5. Befragen Sie Ihre Zielgruppe
Nachdem Sie den prozentualen Anteil in Schritt 4 bestimmt haben, wissen Sie, an wie viele Personen Sie die Erhebung versenden müssen, um genügend abgeschlossene Beantwortungen zu erhalten (Schritt 3). Wie wir gesehen haben, ist beim Entwerfen einer ausgewogenen Umfrage die Kenntnis der Fehlermarge (wie auch aller zugehörigen Begriffe wie Stichprobengröße und Konfidenzniveau) ein wesentlicher Faktor. Wenn Sie in der Lage sind, die eben genannten Größen zu ermitteln, können Sie danach beruhigt weitermachen.
Auch interessant: So schätzen Sie Ihre Population
Optimieren Sie dank SurveyMonkey die Fehlerspanne
Mit SurveyMonkey können Sie leicht Ihre Stichprobengröße erhöhen und somit die Fehlermarge senken. SurveyMonkey Audience liefert Ihnen eine leistungsstarke Plattform für die schnelle und effiziente Erfassung hochwertiger Daten von einer Zielgruppe, die Ihrem Zielmarkt entspricht. Möchten Sie ein neues Produkt auf den Markt bringen oder die Kundenzufriedenheit ermitteln? Oder geht es bei Ihnen um wissenschaftliche Forschung? Unsere Plattform hat für alle Anwendungsfälle die nötigen Tools, mit denen Sie Ihre Zielgruppe erreichen und aussagekräftige Antworten bekommen.
Erfassen Sie die richtigen Daten
SurveyMonkey stellt Ihnen die Tools zur Verfügung, die Sie zum Erstellen, Optimieren und Freigeben Ihrer Umfragen benötigen, um die erforderlichen Beantwortungen zu erhalten.